Wcięcie kątowe
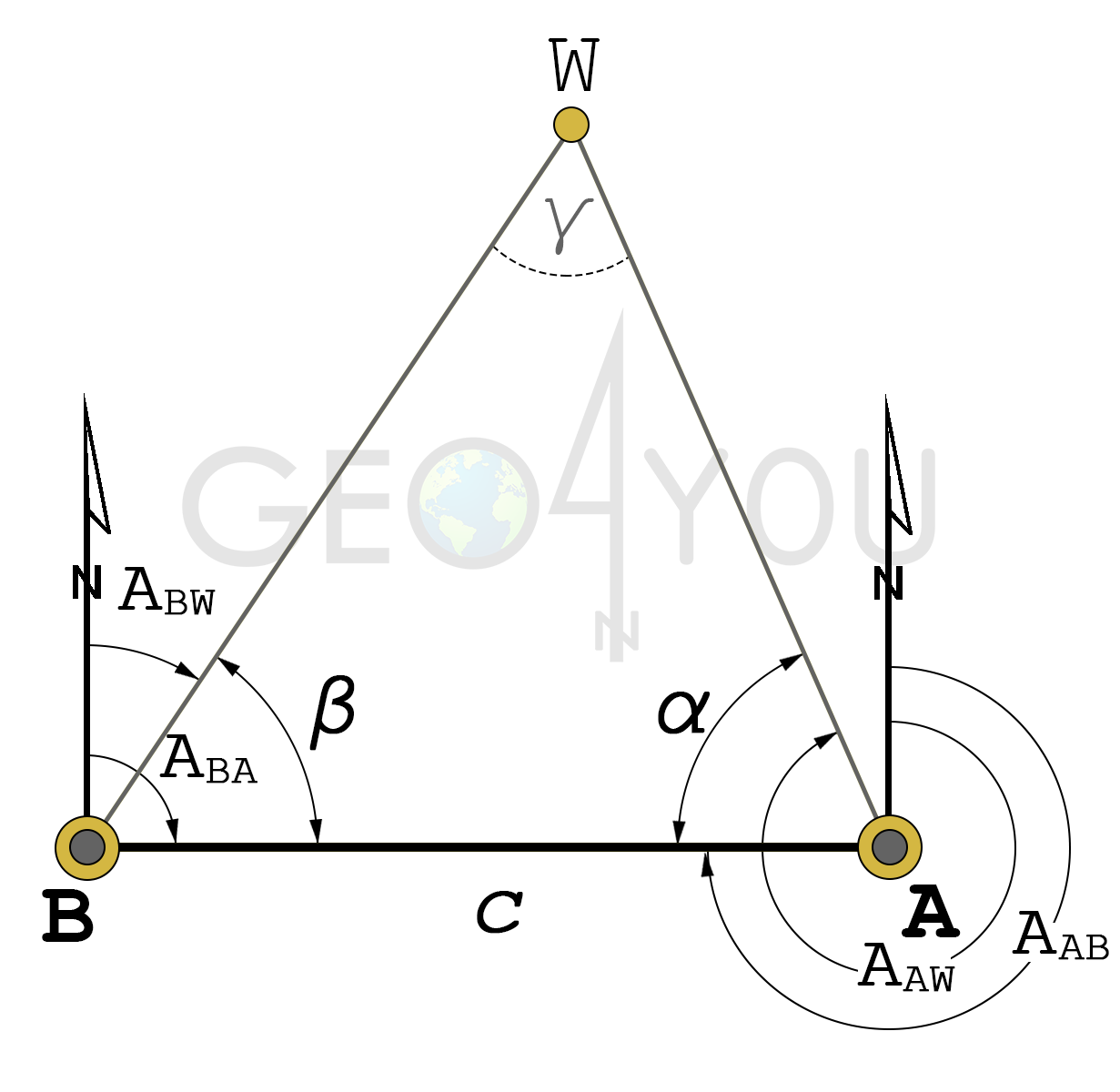
Wcięcie kątowe w przód pozwala wyznaczyć współrzędne punktu wcinanego W na podstawie pomierzonych kątów poziomych α i β ze stanowisk założonych na punktach A i B. Punkty posiadają znane współrzędne, mogą być punktami osnowy pomiarowej. Cała konstrukcja sprowadza się do trójkąta ABW, w którym dwa punkty mają znane współrzędne, a współrzędne trzeciego punktu należy obliczyć. Bazę główną wcięcia stanowi odcinek AB, natomiast odcinki AW i BW są celowymi w przód. Rozwiązanie wcięcia jest jednoznaczne, ponieważ znane są trzy elementy geometryczne trójkąta ABW: długość bazy dAB obliczona ze współrzędnych punktów A, B oraz dwie obserwacje kątowe: α i β.
Obliczenia związane z uzyskaniem wartości długości boków AW i BW przeprowadzone zostały na podstawie twierdzenia sinusów, korzystając z pomierzonych wartości kątów α i β w trójkącie ABW. Wszystkie etapy obliczeń zostały zaprezentowane w odpowiednich komórkach tabeli w celu weryfikacji własnych obliczeń.
Liczby zmiennoprzecinkowe należy wpisywać używając kropki jako znaku wydzielającego część dziesiętną.
Wartości kątów należy podać w gradach.
Przykład
Dane
A: X=100.00m,Y=100.00m
B: X=0.00m,Y=100.00m
Kąt α=50.0000grad
Kąt β=50.0000grad
Szukane
W: X=?m,Y=?m
Szkic